Fractions are a fundamental concept in mathematics, often encountered in daily life, from slicing a pizza to calculating discounts. Among these, "8/15 simplified" represents a fraction that has already been reduced to its simplest form, showcasing the beauty of mathematical precision. Understanding such fractions not only aids in solving mathematical problems but also helps in visualizing portions, making complex calculations more approachable.
In this article, we’ll take a deep dive into the concept of simplifying fractions, with a special focus on "8/15 simplified." We will explore its meaning, its applications, and how it fits into the broader framework of mathematics. Whether you're a student brushing up on your math skills or a curious learner, this guide will equip you with the knowledge to handle fractions like a pro.
With a user-friendly approach, we’ll answer questions such as "What does simplification mean?" and "Why is 8/15 already simplified?" Additionally, we’ll break down related concepts like greatest common divisors, real-world examples of fractions, and tips for simplifying complex fractions. Let’s get started and make fractions less intimidating, one step at a time.
Table of Contents
- What is a Fraction?
- What Does 8/15 Simplified Mean?
- Is 8/15 the Simplest Form?
- How Do You Simplify a Fraction?
- Why is Simplification Important?
- The Role of Greatest Common Divisor in Simplification
- Step-by-Step Guide to Simplifying Fractions
- Real-World Examples of 8/15
- Common Mistakes to Avoid When Simplifying
- How 8/15 Relates to Decimals and Percentages
- Can 8/15 Be Used in Equations?
- Teaching 8/15 Simplified to Kids
- Advanced Concepts Related to 8/15
- Frequently Asked Questions (FAQs)
- Conclusion
What is a Fraction?
Fractions are numerical expressions representing a part of a whole. They consist of two numbers: a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts are being considered, while the denominator specifies the total number of equal parts that make up the whole.
For example, in the fraction 8/15, the numerator is 8, and the denominator is 15. This means we are considering 8 parts out of a total of 15. Fractions can be proper (numerator smaller than denominator), improper (numerator larger than denominator), or mixed (a whole number combined with a fraction). Understanding these basics is essential before delving into simplification.
What Does 8/15 Simplified Mean?
The term "simplified" in mathematics refers to reducing a fraction to its simplest form. A fraction is in its simplest form when the numerator and denominator have no common factors other than 1. In the case of 8/15, the greatest common divisor (GCD) of 8 and 15 is 1, meaning they share no other factors. Therefore, 8/15 is already in its simplest form.
Understanding why a fraction is simplified requires knowledge of prime numbers and factorization. In this context, 8 (2 x 2 x 2) and 15 (3 x 5) have no overlapping prime factors, affirming that 8/15 cannot be reduced further. This makes it an excellent example of a fraction that doesn’t need further simplification.
Is 8/15 the Simplest Form?
Yes, 8/15 is indeed the simplest form. To confirm, we use the GCD method. By identifying the greatest common divisor of the numerator (8) and the denominator (15), we ensure no further reduction is possible. Since their GCD is 1, 8/15 is already simplified.
Another way to verify this is by dividing both the numerator and denominator by their GCD. If the resulting fraction equals the original, it confirms the simplest form. For 8/15, dividing both by 1 yields the same fraction, proving no further simplification is necessary.
How Do You Simplify a Fraction?
Simplifying a fraction involves reducing it to its simplest form. Here’s how you can do it:
- Find the GCD of the numerator and denominator.
- Divide both the numerator and denominator by the GCD.
- Check if the resulting fraction can be reduced further.
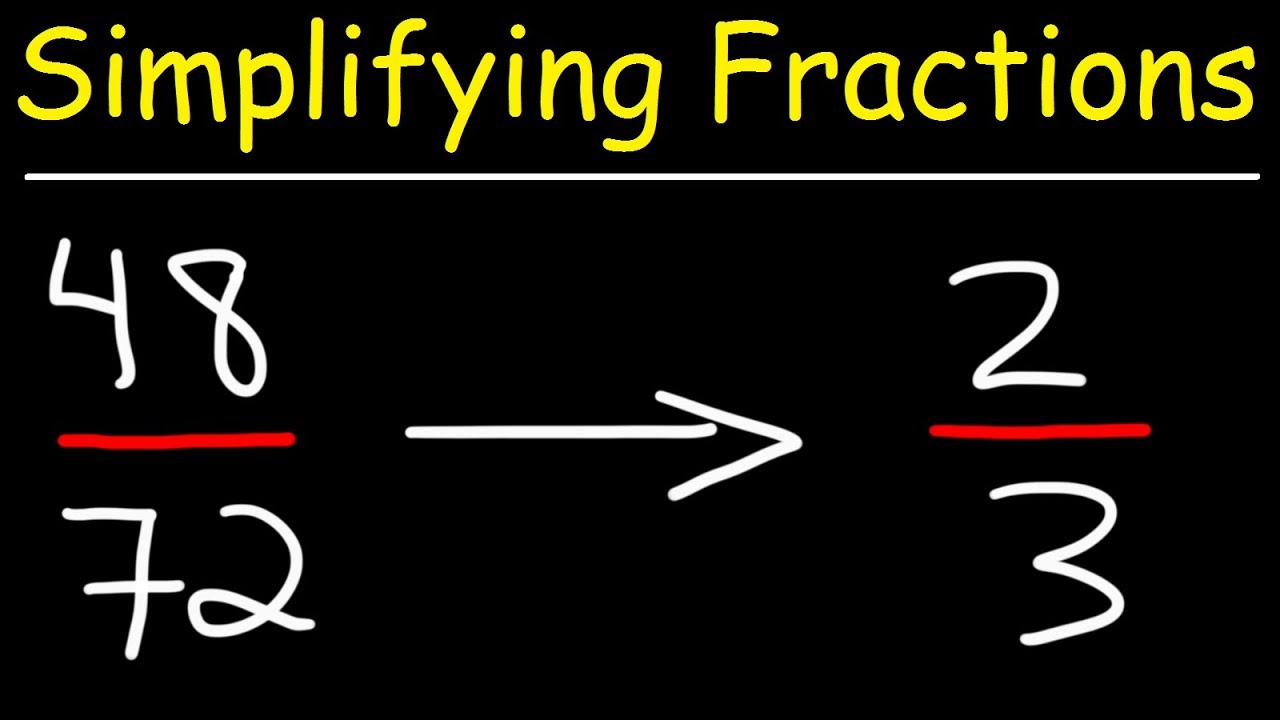
For example, to simplify 24/36:
- Identify the GCD: The GCD of 24 and 36 is 12.
- Divide both numbers by 12: 24 ÷ 12 = 2, and 36 ÷ 12 = 3.
- The simplified fraction is 2/3.
Using this method ensures accuracy and clarity when working with fractions.
Why is Simplification Important?
Simplifying fractions is crucial for several reasons:
- It makes calculations easier and more efficient.
- Simplified fractions are more aesthetically pleasing and easier to interpret.
- They provide clarity, especially when comparing fractions or solving equations.
For instance, 8/15 is easier to understand and use in calculations than a more complex equivalent like 16/30. Simplification also helps in real-life scenarios, such as dividing resources or measuring ingredients.
The Role of Greatest Common Divisor in Simplification
The GCD plays a pivotal role in simplifying fractions. By identifying the largest number that evenly divides both the numerator and denominator, we can reduce the fraction to its simplest form. The GCD ensures that the simplification process is accurate and efficient.
For example, in 8/15, the GCD is 1. Dividing both the numerator and denominator by 1 confirms that the fraction is already simplified. Understanding the GCD is essential for mastering fraction simplification.
Step-by-Step Guide to Simplifying Fractions
Simplifying fractions can be broken down into a few simple steps:
- Find the GCD of the numerator and denominator.
- Divide both numbers by the GCD.
- Verify that the resulting fraction is in its simplest form.
Let’s apply this to 18/24:
- GCD: The GCD of 18 and 24 is 6.
- Divide: 18 ÷ 6 = 3, and 24 ÷ 6 = 4.
- Simplified fraction: 3/4.
Real-World Examples of 8/15
Fractions like 8/15 appear in various real-world scenarios:
- Cooking recipes that require portions of ingredients.
- Dividing resources, such as splitting a pizza into 15 slices and taking 8.
- Measuring distances or weights.
Understanding fractions helps us navigate these situations with ease and precision.
Common Mistakes to Avoid When Simplifying
While simplifying fractions, avoid these common errors:
- Forgetting to find the GCD.
- Incorrectly dividing the numerator or denominator.
- Overlooking the need to simplify further.
Double-checking your work ensures accuracy and prevents mistakes.
How 8/15 Relates to Decimals and Percentages
To convert 8/15 to a decimal:
- Divide 8 by 15: 8 ÷ 15 = 0.5333 (repeating).
To convert to a percentage, multiply the decimal by 100: 0.5333 x 100 = 53.33%.
Can 8/15 Be Used in Equations?
Yes, 8/15 can be used in various mathematical equations, such as:
- Adding or subtracting fractions.
- Multiplying or dividing fractions.
- Solving algebraic equations.
Its simplified form makes calculations more straightforward.
Teaching 8/15 Simplified to Kids
When teaching kids about 8/15 simplified:
- Use visual aids, like pie charts or fraction bars.
- Explain the concept of GCD in simple terms.
- Provide plenty of practice problems.
Interactive methods make learning fractions enjoyable and effective.
Advanced Concepts Related to 8/15
For advanced learners, 8/15 can lead to discussions about:
- Rational numbers and their properties.
- Operations with fractions in higher mathematics.
- Applications in fields like engineering and finance.
Understanding these concepts broadens the scope of knowledge about fractions.
Frequently Asked Questions (FAQs)
1. What is the simplest form of 8/15?
The simplest form of 8/15 is 8/15, as it cannot be reduced further.
2. How do you know if a fraction is simplified?
If the numerator and denominator have no common factors other than 1, the fraction is simplified.
3. Can 8/15 be converted to a decimal?
Yes, 8/15 can be converted to a decimal: 8 ÷ 15 = 0.5333 (repeating).
4. What is the percentage equivalent of 8/15?
The percentage equivalent of 8/15 is 53.33%.
5. Why is it important to simplify fractions?
Simplifying fractions makes calculations easier and provides clarity in mathematical expressions.
6. Are 8/15 and 16/30 equivalent?
Yes, 8/15 and 16/30 are equivalent fractions, but 8/15 is the simplest form.
Conclusion
Fractions, like 8/15 simplified, are an integral part of mathematics and everyday life. Understanding how to simplify fractions enhances problem-solving skills and provides clarity in various contexts. From basic arithmetic to advanced applications, mastering fractions is a valuable skill. By following the steps and tips outlined in this guide, you’ll be well-equipped to tackle fractions with confidence and ease.